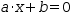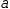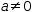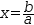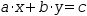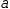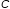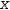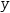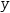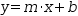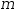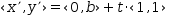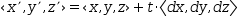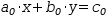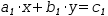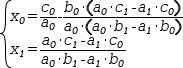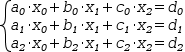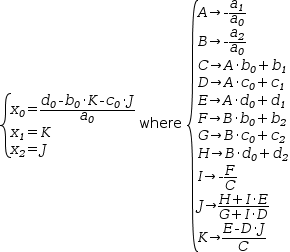5.1 Linear forms
A magnitude can be written as a linear equation with only one
variable:
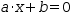 a⋅x+b=0, where
a⋅x+b=0, where
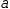 a
and
a
and
 b
are
constants and
b
are
constants and
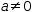 a≠0. This equation has the solution
a≠0. This equation has the solution
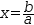 x=b÷a.
x=b÷a.
A line can be written as a linear equation with two variables:
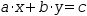 a⋅x+b⋅y=c
where
a⋅x+b⋅y=c
where
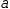 a,
a,
 b
and
b
and
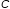 c
are constants and
c
are constants and
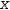 x
and
x
and
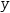 y
are variables.
Isolating
y
are variables.
Isolating
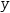 y, the equation becomes
y, the equation becomes
 y=-(a÷b)⋅x+c÷b
which has the familiar form
y=-(a÷b)⋅x+c÷b
which has the familiar form
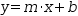 y=m⋅x+b, where
y=m⋅x+b, where
 b
is
a point on the y-axis and
b
is
a point on the y-axis and
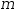 m
is the slope of the line.
In parametric form, this expression is
m
is the slope of the line.
In parametric form, this expression is
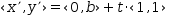 (x’, y’)ʋ=(0, b)ʋ+t⋅(1, 1)ʋ.
In 3-space,
a line can be represented by a point and an
attitude
– the
slope in two directions:
(x’, y’)ʋ=(0, b)ʋ+t⋅(1, 1)ʋ.
In 3-space,
a line can be represented by a point and an
attitude
– the
slope in two directions:
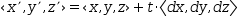 (x’, y’, z’)ʋ=(x, y, z)ʋ+t⋅(dx, dy, dz)ʋ.
(x’, y’, z’)ʋ=(x, y, z)ʋ+t⋅(dx, dy, dz)ʋ.
Two lines in Cartesian space, not parallel, must cross at one point.
The general expression for the intersection
of two lines
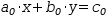 a_0⋅x+b_0⋅y=c_0
and
a_0⋅x+b_0⋅y=c_0
and
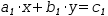 a_1⋅x+b_1⋅y=c_1
is
a_1⋅x+b_1⋅y=c_1
is
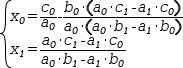 (x_0=c_0÷a_0-b_0⋅(a_0⋅c_1-a_1⋅c_0)÷(a_0⋅(a_0⋅b_1-a_1⋅b_0)), x_1=(a_0⋅c_1-a_1⋅c_0)÷(a_0⋅b_1-a_1⋅b_0))ℓ.
(x_0=c_0÷a_0-b_0⋅(a_0⋅c_1-a_1⋅c_0)÷(a_0⋅(a_0⋅b_1-a_1⋅b_0)), x_1=(a_0⋅c_1-a_1⋅c_0)÷(a_0⋅b_1-a_1⋅b_0))ℓ.
m
lines in
n
-space can be represented by a set of linear equations.
If each is neither parallel to nor coincident with any of the others,
they
may
cross at one point.
If they do,
a single solution to the set of linear equations exists.
The general expression for the intersection of three lines given by
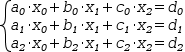 (a_0⋅x_0+b_0⋅x_1+c_0⋅x_2=d_0, a_1⋅x_0+b_1⋅x_1+c_1⋅x_2=d_1, a_2⋅x_0+b_2⋅x_1+c_2⋅x_2=d_2)ℓ
(a_0⋅x_0+b_0⋅x_1+c_0⋅x_2=d_0, a_1⋅x_0+b_1⋅x_1+c_1⋅x_2=d_1, a_2⋅x_0+b_2⋅x_1+c_2⋅x_2=d_2)ℓ
is
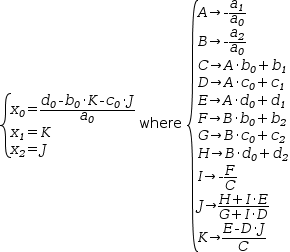 (A.→-(a_1÷a_0), B.→-(a_2÷a_0), C.→A.⋅b_0+b_1, D.→A.⋅c_0+c_1, E.→A.⋅d_0+d_1, F.→B.⋅b_0+b_2, G.→B.⋅c_0+c_2, H.→B.⋅d_0+d_2, I.→-(F.÷C.), J.→(H.+I.⋅E.)÷(G.+I.⋅D.), K.→(E.-D.⋅J.)÷C., (x_0=(d_0-b_0⋅K.-c_0⋅J.)÷a_0, x_1=K., x_2=J.)ℓ),
(A.→-(a_1÷a_0), B.→-(a_2÷a_0), C.→A.⋅b_0+b_1, D.→A.⋅c_0+c_1, E.→A.⋅d_0+d_1, F.→B.⋅b_0+b_2, G.→B.⋅c_0+c_2, H.→B.⋅d_0+d_2, I.→-(F.÷C.), J.→(H.+I.⋅E.)÷(G.+I.⋅D.), K.→(E.-D.⋅J.)÷C., (x_0=(d_0-b_0⋅K.-c_0⋅J.)÷a_0, x_1=K., x_2=J.)ℓ),
which is computable, but not particularly helpful.
Another kind of solution has lines in pairs each defining a plane, where the
solution is the line
of intersection between them.